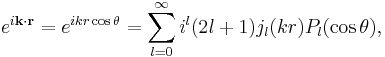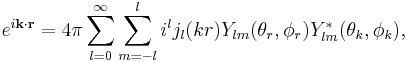Plane wave expansion

In physics the plane wave expansion expresses a plane wave as a sum of spherical waves,

$e^{i\mathbf{k}\cdot\mathbf{r}} = e^{ikr\cos\theta}=\sum_{l=0}^\infty i^l (2l%2B1) j_l(kr)P_l(\cos\theta),$

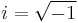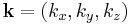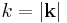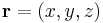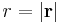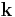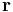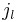where $i=\sqrt{-1}$ . The wave vector $\mathbf{k}=(k_x,k_y,k_z)$ has length $k=|\mathbf{k}|$ and the vector $\mathbf{r}=(x,y,z)$ has length $r=|\mathbf{r}|$ . The angle between the vectors $\mathbf{k}$ and $\mathbf{r}$ is $\theta$ . The functions $j_l$ are Sperical Bessel functions and 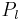$P_l$ are Legendre polynomials.

With the spherical harmonic addition theorem the equation can be rewritten as

$e^{i\mathbf{k}\cdot\mathbf{r}} = 4\pi\sum_{l=0}^\infty\sum_{m=-l}^l i^l j_l(kr) Y_{lm}(\theta_r,\phi_r)Y^\ast_{lm}(\theta_k,\phi_k),$

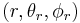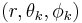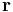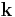where $(r,\theta_r,\phi_r)$ and $(r,\theta_k,\phi_k)$ are the spherical coordinates of the vectors $\mathbf{r}$ and $\mathbf{k}$ , respectively, and the functions 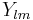$Y_{lm}$ are spherical harmonics.

Applications

The plane wave expansion is applied in

Acoustics
Optics
Quantum scattering theory

References

Digital Library of Mathematical Functions, Equation 10.60.7, National Institute of Standards and Technology, http://dlmf.nist.gov/10.60.E7
Rami Mehrem, The Plane Wave Expansion, Infinite Integrals and Identities Involving Spherical Bessel Functions, http://arxiv.org/abs/0909.0494

Plane wave expansion

Applications

See also

References